Inecuaciones (5)

En entradas anteriores hemos visto cómo resolver inecuaciones por diferentes métodos. Vamos a etudiar varios ejemplos más donde se nos presentarán algunos casos más complejos.

En todos ellos, se propone comprobar los resultados mediante el método gráfico. Basta con hacer un sencillo Copiar + Pegar en la barra de búsqueda de Google con las expresiones que se indican.

 Ejemplo #1 | 3x^2 + 6x + 13 > (x + 3)^2. 

Para resolver este tipo de inecuación (2º grado) vamos a llevar todos los términos al miembro de la izquierda, dejando cero en el de la derecha. Así pues:

3x^2 + 6x + 13 > x^2 + 6x + 9 ;

 2x^2 + 4 > 0 

Una vez obtenida esa expresión, la convertimos en una ecuación reemplazando el signo ">" por un signo igual.

2x^2 + 4 = 0

Si intentamos resolver esa ecuación incompleta de 2º grado, llegamos a la conclusión de que no tiene solución. Por tanto, no tenemos ninguna solución con la que marcar la recta real y dividirla en varios intervalos. Debido a esto, todos los números reales se comportarán del mismo modo en cuanto al signo de su resultado. Como son válidos los valores de "x" que logran que la expresión de la izquierda tome valores positivos, la solución será:

• Gráficamente:
  
• Paréntesis y corchetes: (-∞, +∞)
• Comprobar en Google:  y = 2x^2 + 4 
  

 Ejemplo #2 | x^3 + 2x^2 ≥ 0. 

Para resolver este tipo de inecuación (3er grado) podemos saltarnos el primer paso, ya que todos los términos se encuentran en el miembro de la izquierda y tenemos cero en el de la derecha. Así pues:

 x^3 + 2x^2 ≥ 0 

Una vez obtenida esa expresión, la convertimos en una ecuación reemplazando el signo "≥" por un signo igual.

x^3 + 2x^2 = 0 ;
x^2·(x + 2) = 0

Si resolvemos esa ecuación de tercer grado obtenemos dos soluciones, x = 0 (doble) y x = -2. Llevamos nuestras soluciones a la recta real y analizamos el signo de cada uno de sus tres trozos tomando un valor al azar de cada intervalo. Como son válidos los valores de "x" que logran que la expresión de la izquierda tome valores positivos, la solución será:

• Gráficamente:
  
• Paréntesis y corchetes: [-2, +∞)
• Comprobar en Google:  y = x^3 + 2x^2 

 Ejemplo #3 | x^4 + 2x^2 - 3 < 0. 

Para resolver este tipo de inecuación (4º grado) podemos saltarnos el primer paso, ya que todos los términos se encuentran en el miembro de la izquierda y tenemos cero en el de la derecha. Así pues:

 x^4 + 2x^2 - 3 < 0 

Una vez obtenida esa expresión, la convertimos en una ecuación reemplazando el signo "<" por un signo igual.

x^4 + 2x^2 - 3 = 0

Si resolvemos esa ecuación de cuarto grado obtenemos dos soluciones, x =-1 y x = 1. Las otras dos soluciones son no reales (NR). Las llevamos a la recta real y analizamos el signo de cada uno de sus tres trozos tomando un valor al azar de cada intervalo. Como son válidos los valores de "x" que logran que la expresión de la izquierda tome valores negativos, la solución será:

• Gráficamente:
  
• Paréntesis y corchetes: (-1, 1)
• Comprobar en Google:  y = x^4 + 2x^2 - 3 

 Ejemplo #4 | -x^3 + 13x + 12 ≥ 0. 

Para resolver este tipo de inecuación (3er grado) podemos saltarnos el primer paso, ya que todos los términos se encuentran en el miembro de la izquierda y tenemos cero en el de la derecha. Así pues:

 -x^3 + 13x + 12 ≥ 0 

Una vez obtenida esa expresión, la convertimos en una ecuación reemplazando el signo "≥" por un signo igual.

-x^3 + 13x + 12 = 0

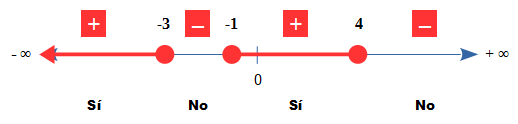
Podemos resolver usando la regla de Ruffini, logrando tres soluciones: x = -3, x = -1 y x = 4. Las llevamos a la recta real y analizamos el signo de cada uno de sus cuatro trozos tomando un valor al azar de cada intervalo. Como son válidos los valores de "x" que logran que la expresión de la izquierda tome valores positivos, la solución será: 

• Gráficamente:
  
• Paréntesis y corchetes: (-∞, -3] U [-1, 4]
• Comprobar en Google:  y = -x^3 + 13x + 12  

 

 Ejemplo #5 | x^2 + x + 5 < 0. 

Para resolver este tipo de inecuación (2º grado) podemos saltarnos el primer paso, ya que todos los términos se encuentran en el miembro de la izquierda y tenemos cero en el de la derecha. Así pues:

 x^2 + x + 5 < 0 

Una vez obtenida esa expresión, la convertimos en una ecuación reemplazando el signo "<" por un signo igual.

x^2 + x + 5 = 0

Cuando intentamos encontrar la solución de esta ecuación aplicando la fórmula de la ecuación de 2º grado, obtenemos un discriminante negativo. Por tanto, la ecuación no tiene solución y no tenemos valores que llevar a la recta real. De nuevo, todos los números reales darán resultados con el mismo signo Como son válidos los valores de "x" que logran que la expresión de la izquierda tome valores negativos, la solución será:

• Gráficamente:
  
• Paréntesis y corchetes: No tiene solución.
• Comprobar en Google:  y = x^2 + x + 5 

Al igual que sucede con las ecuaciones y los sistemas de ecuaciones, algunos casos no tienen solución. No hay ningún número real que verifique la expresión del enunciado.