Inecuaciones (6). El uso de la calculadora.

En ocasiones, resolver una inecuación implica la realización de gran cantidad de cálculos que, a veces, pueden resultar bastante complejos. Cuando analizamos el signo de los resultados de cada intervalo para decidir si forma parte o no de la solución podemos tropezar con operaciones muy complicadas, tanto si las realizamos mentalmente como sobre el papel.

Sin duda, llegado este momento, podemos afirmar que la calculadora es un gran invento. Aunque en ciertas situaciones abusamos de su utilización, este es uno de los casos en los que usarla está totalmente justificado: necesitamos realizar gran cantidad de cálculos y no disponemos de demasiado tiempo. No importa la marca o el modelo de nuestra calculadora. Por rudimentaria que sea, se convertirá en una gran aliada.

La mayoría de las calculadoras actuales disponen de una pantalla con dos partes bien diferenciadas. La primera podemos denominarla línea de comandos, que aparece en la franja superior. Ahí es donde debemos indicar a la calculadora qué operaciones hacer y en qué orden efectuarlas. La segunda es la línea de resultados, donde nos muestra el valor obtenido tras pulsar la tecla  = .

Por otra parte, disponemos de un botón con el rótulo  ANS  (procedente del término inglés answer, respuesta) que nos permite un acceso rápido y totalmente exacto al último resultado que hayamos conseguido en la pantalla. La combinación de este botón junto con las opciones de navegación de los cursores de desplazamiento nos abren un mundo lleno de posibilidades.

Vamos a resolver un ejemplo estudiado en la entrada anterior y explicaremos cómo agilizar los cálculos mediante el uso de la calculadora.

 Inecuaciones (5) | Ejemplo #4 | -x^3 + 13x + 12 ≥ 0. 

Para resolver este tipo de inecuación (3er grado) podemos saltarnos el primer paso, ya que todos los términos se encuentran en el miembro de la izquierda y tenemos cero en el de la derecha. Así pues:

 -x^3 + 13x + 12 ≥ 0 

Una vez obtenida esa expresión, la convertimos en una ecuación:

-x^3 + 13x + 12 = 0

Resolvemos por Ruffini, encontrando tres soluciones: x = -3, x = -1 y x = 4. Las llevamos a la recta real y analizamos el signo de cada uno de sus cuatro trozos tomando un valor al azar de cada intervalo.

Vamos a explicar la secuencia de operaciones que debemos introducir en nuestra calculadora para lograr una tabla de valores de forma rápida y sencilla.

• Escogemos un valor del intervalo (-∞, -3), x = -5. Para introducirlo en la calculadora, teclearemos:  -   5   = . Aparecerá el valor -5 en la línea de resultados.
• Vamos a evaluar la expresión de la inecuación en x = -5. En lugar de escribir directamente ese valor, como es el último resultado en pantalla, lo usaremos mediante la tecla  ANS  cada vez que corresponda escribir la incógnita "x". Así pues, debemos expresarlo como:

 -   ANS   ^   3    +   13   ANS   +   12    = 

• El resultado obtenido es 72, por lo que el signo del intervalo será  + .
• Escogemos un valor del intervalo (-3, -1), x = -2. Para introducirlo en la calculadora, teclearemos:  -   2   = . Aparecerá el valor -2 en la línea de resultados.
• Para evaluar la expresión no será necesario volver a escribir todo. Basta con usar la flecha del cursor que apunta hacia arriba  ⇧  y aparecerá en pantalla la expresión completa que escribimos en el paso anterior. Sin embargo, la calculadora tomará el valor de  ANS  como el último resultado en pantalla, es decir, x = -2.
• El resultado obtenido es -6, por lo que el signo del intervalo será  - .
• Escogemos un valor del intervalo (-1, 4), x = 3. Para introducirlo en la calculadora, teclearemos:  3   = . Aparecerá el valor 3 en la línea de resultados.
• Pulsamos la flecha del cursor que apunta hacia arriba  ⇧  y aparecerá en pantalla de nuevo la expresión que queremos evaluar. La calculadora tomará el valor de  ANS  como el último resultado en pantalla, es decir, x = 3.
• El resultado obtenido es 24, por lo que el signo del intervalo será  + . 
• Escogemos un valor del intervalo (4, +∞), x = 6. Para introducirlo en la calculadora, teclearemos:  6   = . Aparecerá el valor 6 en la línea de resultados. 
• Pulsamos la flecha del cursor que apunta hacia arriba  ⇧  y aparecerá en pantalla de nuevo la expresión que queremos evaluar. La calculadora tomará el valor de  ANS  como el último resultado en pantalla, es decir, x = 6. 
• El resultado obtenido es -126, por lo que el signo del intervalo será  - .

Como son válidos los valores de "x" que logran que la expresión de la izquierda tome valores positivos, la solución será:

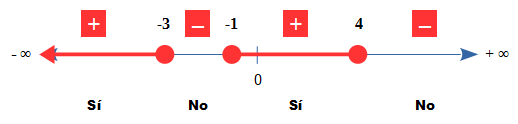
• Gráficamente:
  
• Paréntesis y corchetes: (-∞, -3] U [-1, 4]
• Comprobar en Google:  y = -x^3 + 13x + 12