Algunas ecuaciones exponenciales presentan incógnitas en más de un exponente. A diferencia de otras ecuaciones exponenciales más sencillas, en este tipo vamos a tener que recurrir a un recurso, el cambio de variable, que ya hemos utilizado en otras ecuaciones de la Unidad 3. Es imprescindible que todas las potencias que tienen alguna incógnita en el exponente posean la misma base para realizar ese cambio de variable.
Ejemplo #1 | 2^(x+1) + 2^(x-2) - 18 = 0
Ejemplo #1 | 2^(x+1) + 2^(x-2) - 18 = 0
Para resolver esta ecuación debemos, en primer lugar, aplicar las propiedades de las potencias con la intención de dejar las expresiones exponenciales lo más simples posible. Así obtenemos que:
Llegado este punto, vamos a aplicar el cambio de variable. En concreto, para nuestra ecuación, ese cambio de variable consistirá en t = 2^x (siempre la expresión exponencial más sencilla), de modo que la ecuación resultante es de 1er grado con denominadores. Una vez hecho el MCM:
La solución de la ecuación es t = 8, pero "t" no es la solución de la ecuación original. Para hallar el resultado de la "x", debemos deshacer el cambio de variable, de manera que obtenemos una ecuación exponencial sencilla:
Se logra una única solución: x = 3. Tras llevarla a la ecuación original, vemos que es válida.
Ejemplo #2 | 4^x - 5·2^x + 4 = 0
Para resolver esta ecuación debemos de expresar todos los términos que poseen "x" en el exponente como potencias con la misma base. La potencia 4^x se puede expresar como 2^(2x), logrando:
Ejemplo #2 | 4^x - 5·2^x + 4 = 0
Para resolver esta ecuación debemos de expresar todos los términos que poseen "x" en el exponente como potencias con la misma base. La potencia 4^x se puede expresar como 2^(2x), logrando:
Si aplicamos el cambio de variable t = 2^x, obtenemos una ecuación polinómica de 2º grado:
La ecuación tiene dos soluciones, t = 4 y t = 1. No obstante, debemos deshacer el cambio de variable:
- Si t = 4 -> 2^x = 4 -> 2^x = 2^2 -> x = 2
- Si t = 1 -> 2^x = 1 -> 2^x = 2^0 -> x = 0


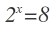


¿Me podrias decir como se pasa de la ecuacion original a la simplificada? Es el paso de la primera foto. Gracias
ResponderEliminarHemos aplicado las propiedades de las potencias. Cuando en el exponente aparecen sumando, las transformamos en un producto: 2^(x+1) = 2^x · 2^1 = 2^x · 2. Cuando en el exponente aparecen restando, las transformamos en un cociente: 2^(x-2) = 2^x / 2^2 = 2^x / 4.
EliminarComo se hace la f del ejercicio 3 de la fotocopia de repaso del tema 3?
ResponderEliminarHola Juan. Por favor,escribe tu comentario en la página sobre la que tienes la duda, así los compañeros podrán localizar el ejercicio más fácilmente.
Eliminar